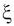
Пусть случайная величина распределена по нормальному закону,
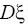
для которого дисперсия неизвестна. Делается выборка объема n . Из
нее определяется исправленная выборочная дисперсия s². Случайная
величина



распределена по закону X² c n –1 степенями свободы. По заданной
надежности y можно найти сколько угодно границ X₁² и X₂² интервалов,
таких, что



Найдем X₁² и X₂² из следующих условий:



Очевидно, что при выполнении двух последних условий справедливо
равенство (*).
В таблицах для случайной величины X² обычно дается решение
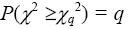
уравнения . Из такой таблицы по заданной величине q и по
числу степеней свободы n – 1 можно определить значение X_q². Таким
образом, сразу находится значение X₂² в формуле (***).